Calcular a Circunferência da Terra

Os Gregos

Hoje em dia seria uma tarefa fácil para um cientista calcular a circunferência da Terra, pois existem vários aparelhos e tecnologias que podem ajudar nesta tarefa. Mesmo assim, imagine que alguém peça para você calcular a circunferência de nosso planeta, sem ter em mãos nenhum tipo de medidor ou tecnologia, ou até mesmo sem uma fórmula? Se esta pergunta fosse feita hoje, a esmagadora maioria das pessoas iria errar a resposta, ou então nem responder. No entanto, na Grécia um astrônomo conseguiu responder esta pergunta usando apenas seu raciocínio lógico e seu extenso conhecimento matemático. Este incrível homem foi Erastóstenes, que nasceu em 276 antes de Cristo e morreu 194 antes de Cristo.

Perimetro

A Descoberta de Erastóstenes

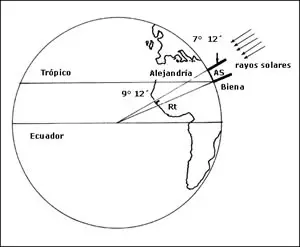
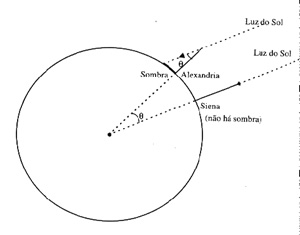
O astrônomo observou que as sombras projetadas por postes de cidades diferentes e a uma determinada distância uma da outra projetavam sombras com tamanhos e inclinações diferentes ao meio dia. Como o horário era o mesmo (meio-dia) a única explicação possível era de que as cidades ficavam em “alturas” diferentes, indicando que a Terra precisaria ser curva. Ou seja, com uma simples observação e pensamento lógico o grego descobriu que a Terra era redonda! Depois que descobriu o fato o astrônomo começou a medir as diferenças dos ângulos das sombras projetadas. Era assim: ele pegou um poste que levava de cidade em cidade. Sempre ao meio dia, colocava o poste reto sobre o chão de uma cidade e media o ângulo formado pela sombra. Depois, repetia o procedimento em outra cidade distante (para que ficasse evidente que a diferença de ângulos e provar que a Terra era mesmo redonda).

Calcular a Circunferência da Terra

As Dificuldades

Logo o astrônomo se deparou com um problema: a luz do sol batia em ângulos diferentes de acordo com a época do ano. Para não invalidar sua pesquisa, o grego fez a medição em uma cidade e exatamente um ano depois, fez a mesma medição mas em uma outra cidade a 800 quilômetros de distância, em direção ao norte. A medição tornou evidente que a diferença era de 7 graus entre uma cidade e outra. Como um globo possui 360 graus, o astrônomo percebeu que precisava multiplicar o número 7 por aproximadamente 50 para dar a circunferência correta.

Comprimento

Como a distância entre as duas cidades era de 800 quilômetros, o grego multiplicou este valor por 50, e obteve uma distância que equivale a 40000 quilômetros. Na realidade a circunferência da Terra possui 40075 quilômetros (sem contar os pólos que são achatados e medem 40008 quilômetros), mas devido ao fato de não existirem equipamentos precisos na época a descoberta do grego é um fato e tanto, pois a margem de erro foi muito pequena.

Neto